문제
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.
출력
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
예제 입력 1
3
4
7
10
예제 출력 1
7
44
274
위 문제를 보면 입력값의 범위는 1~10까지의 범위이며 1,2,3을 더해서 만들 수 있는 수열들의 갯수를 출력하는 문제였습니다. 즉 1번 미리 계산 해놓는다면 이후에 다시 연산할 필요가 없다는 접근에서 시작되었습니다. DP로 해결해야 하지 않을까 하는 생각을 했습니다. DP(Dynamic Programming)로 해결하는 문제들의 공통점은 점화식을 유도해낼 수 있다는 것 입니다.
저는 머리가 좋지 않기 때문에 직접 일부 수들을 손으로 다 적어가면서 규칙을 찾아나가기 시작했습니다. 직접 손으로 적어가면서 찾게 된 규칙은 다음과 같습니다.

D[i] = 입력 받은 수를 말합니다. 입력받은 수가 4이상 일 경우에는 D[i-1]+D[i-2]+D[i-3]의 값과 같다는 것을 유추해냈습니다. 이를 증명하기 위해서 다시 하나의 수를 가지고 다시 보이겠습니다.
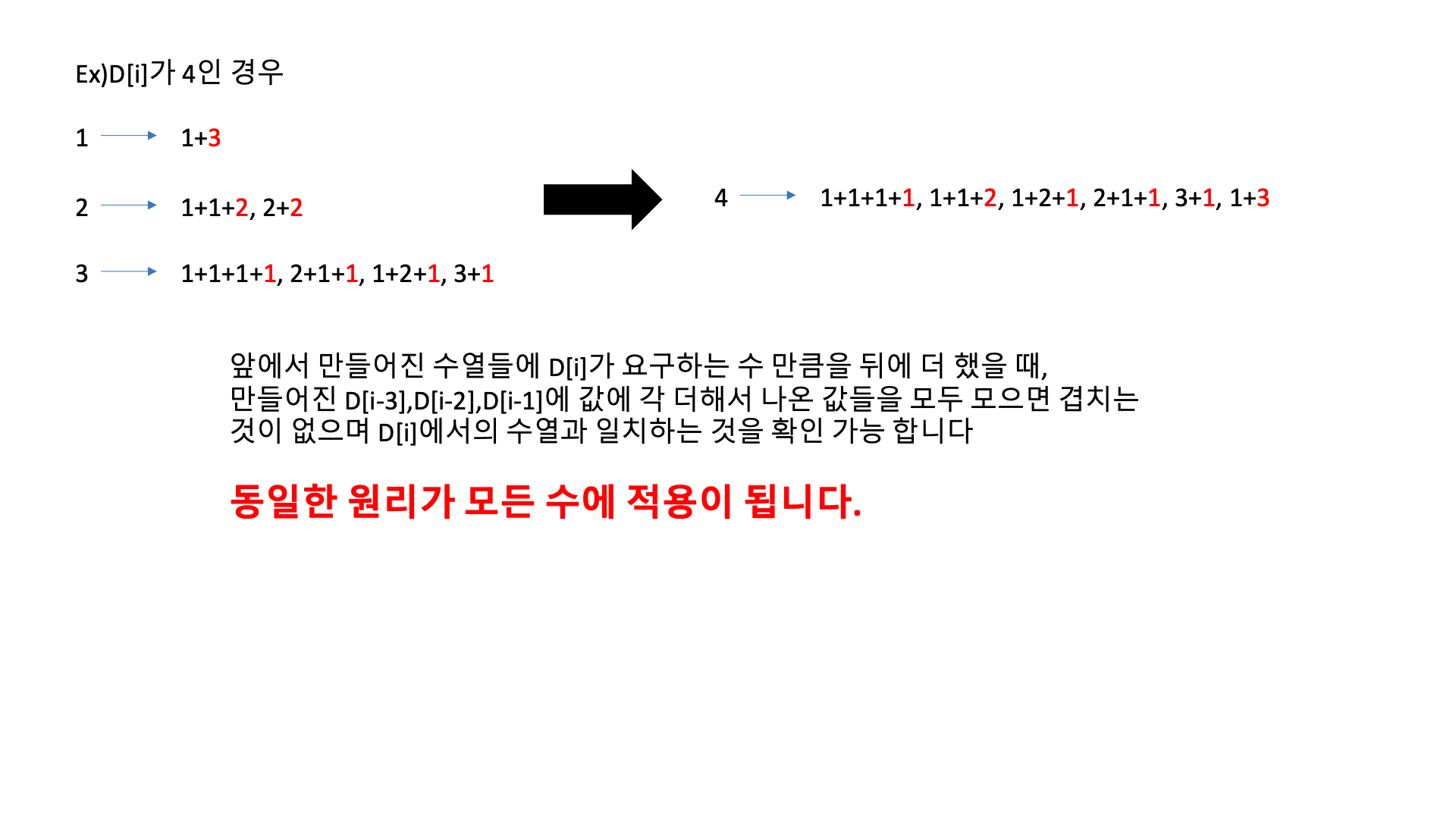
보시는 것 처럼 이미 앞에서 성립된 수열에 입력값보다 부족한 만큼의 수를 더해주었을 때 나오는 수열이 D[i]가 1, 2, 3일때 나오는 것이 겹치지 않습니다. 모두 합쳐주면 D[i] = 4 일 때와 동일하다는 것도 볼 수 있습니다. 위와 같이 D[5]일때도.. D[6]일 때도 동일하게 적용됩니다.
위 입력예제를 보시면 D[7]일때 출력되는 결과는 44입니다.
이는 D[4]+ D[5]+ D[6] = 7+13+24 = 44 입니다.
D[8] = D[5]+D[6]+D[7] = 13+24+44 = 81
D[9] = D[6]+D[7]+D[8] = 24+44+81 = 149
D[10] = D[7]+D[8]+D[9] = 44+81+149 = 274
위 입력예제에서 나오는 값을 모두 일치하는 것을 확인할 수 있습니다.
이를 통해서 우리는 위 문제를 해결하는데 생각했던 점화식이 맞았음을 알 수 있습니다.
코드는 다음과 같습니다.
T = int(input()) # 테스트 갯수
dp = [1,2,4]
for i in range(3,10): # 점화식 계산
dp.append(dp[i-1]+dp[i-2]+dp[i-3])
# print(dp)
ques = [] # 입력 값
for _ in range(T):
num = int(input())
ques.append(num)
for i in ques: # 결과 출력
print(dp[i-1])'알고리즘 > 문제풀이' 카테고리의 다른 글
| 백준 11286번 절대값 힙 - Python (0) | 2023.04.01 |
|---|---|
| 백준 11279번 최대 힙 - Python (0) | 2023.03.22 |
| 백준 11399 ATM - Python (0) | 2023.03.19 |
| 백준 11047번 동전0 - Python (0) | 2023.03.17 |
| 백준 1676번 팩토리얼 0의 개수 : Python (1) | 2023.03.15 |
